Fondamenti – GM Hydro

Premessa

Le turbine idrauliche appartengono alla categoria delle macchine motrici e possono essere classificate in base a vari criteri ma quello più comunemente usato è relativo alla trasformazione dell’ energia che in esse avviene. Le distinguiamo quindi in turbine ad AZIONE e a REAZIONE. Appartengono alla prima categoria le PELTON (fig 1) dove l’energia potenziale, E_p = mgH (m=massa, g= accelerazione di gravità, H= salto) si trasforma in energia cinetica ${ E }_{ c }=\frac { 1 }{ 2 } m{ v }^{ 2 }$ con v= velocità del fluido prima di agire sulle pale della ruota. Ciò significa che il fluido colpisce la girante con velocità $v\cong\sqrt { 2gH }$

fig 1

fig 2

fig 3

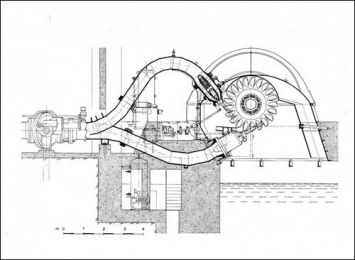
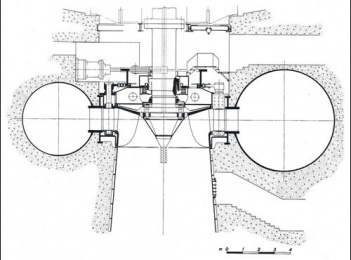
Sono a REAZIONE le turbine FRANCIS (fig 2) e le turbine KAPLAN (fig 3). Alle rispettive giranti è demandato il compito di trasformare in energia cinetica la restante parte di energia potenziale ancora disponibile.

Girante Pelton

Girante Francis

Girante Kaplan

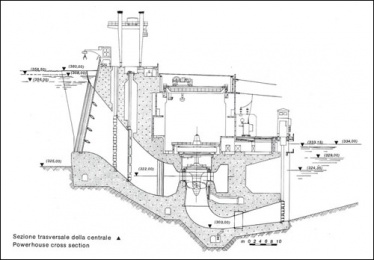
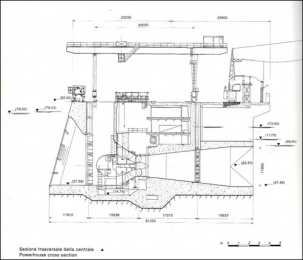
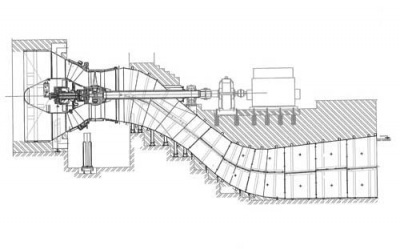
Appartengono a questa categoria anche le turbine BULBO (fig 4) e le turbine S (fig 5) .

fig 4

fig 5

Le prime due grandezze fondamentali necessarie per il dimensionamento di una turbina idraulica sono:
1) H = caduta o salto netto disponibile [m] 2) Q = portata del fluido [m³/s]

fig 6 – misura del salto netto (A) per turbine ad azione (B) per turbine a reazione

Detto $\gamma$ il peso specifico del fluido, $\eta$ il rendimento della turbina la potenza generata dalla turbina espressa in Kw sarà:
P= $\bf\frac {{\large \gamma} QH{\large \eta }}{ 101,97 }$ assunto per l’acqua $\gamma$ = 1000 Kg/m³P ≈ 9,81 Q H η [a]
La stessa espressione può essere usata per il calcolo della potenza del gruppo generatore ma in questo caso il rendimento $\eta$ della turbina va sostituito con quello complessivo ${\eta}_{t}$ ottenuto dal prodotto dei rendimenti dei singoli componenti ( turbina, alternatore, trasformatore ). Infine alla potenza ottenuta dovrà essere sottratta quella relativa alle perdite meccaniche ( es. quelle relative ai supporti) e volumetriche (es. quelle relative allo scarico dell’acqua in pressione fra coperchio e girante)

Numero di Giri Specifico
Supponiamo di avere una turbina funzionante con H, Q, n e di voler utilizzare la stessa girante con un salto H’ diverso da H. La nuova velocità assoluta sarà v’= $\sqrt { 2gH }$ pertanto si potrà scrivere: $\frac {\large v }{\large v' } =\frac { \sqrt { 2gH} }{ \sqrt { 2gH'}} =\sqrt { \frac { H}{ H'} }$
Nelle figure sotto riportate si sono indicati con il pedice 1 le velocità all’ingresso della girante e con 2 quelle all’uscita.

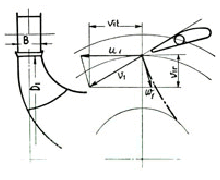
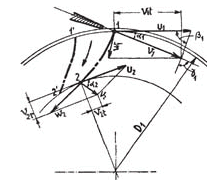
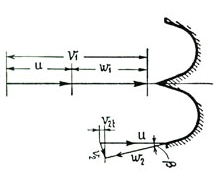
Trattasi di velocità periferica u, assoluta v e relativa w. Affinché tutto funzioni regolarmente dovrà sussistere l’eguaglianza:   $\frac {\large v }{\large v' } =\frac {\large u}{\large u'}=\frac {\large w}{\large w'} =\sqrt { \frac { H}{ H'} }$
Dato che la girante non è cambiata anche la portata attraverso il canale palare dovrà variare in funzione della nuova velocità w’. Conseguentemente potremo scrivere :   $\frac {\large w }{\large w' } =\frac { Q}{ Q'} =\sqrt { \frac { H}{ H'} }$
La velocità periferica u è legata al numero di giri e parimenti potremo scrivere : $\frac {\large u }{\large u' } =\frac {\large n}{\large n'} =\sqrt { \frac { H}{ H'} }$
A conclusione di quanto sopra potremo affermare che la ruota funzionante con H, Q, n funzionerà altrettanto bene con H’, Q’, n’
Ancora, quanto sopra espresso ci permette di fare un’altra importante considerazione.
La stessa girante anziché operare sotto il salto H facciamola funzionare sotto il salto di 1 m. Applicando pari pari le relazioni precedenti ed indicando con pedice 1 i valori relativi alle nuove condizioni possiamo scrivere:
$\frac { Q}{{ Q}_{1}} =\sqrt { \frac { H}{ 1} }$       Q₁= $\bf\frac { Q}{ \sqrt { H}}$                $\frac {\large n}{{\large n}_{1}} =\sqrt { \frac { H}{ 1} }$                    n₁= $\bf\frac {\large n}{ \sqrt { H}}$
Ora vediamo come le relazioni precedenti ci permettono di scriverne quelle relative al cambiamento del diametro della girante passando dal valore D al valore di 1 m. Tutte le dimensioni geometriche della ruota varieranno nello stesso rapporto fino ad ottenere il diametro di 1m. Sappiamo che il salto è H =1 m e quindi la velocità assoluta all’ingresso della nuova ruota sarà la stessa rispetto a quella di diametro D. Ciò ci permette di affermare che anche le altre velocità rimarranno invariate perché legate fra di loro dal triangolo delle velocità ( vedi fig. sopra).

Le velocità abbiamo visto che non sono cambiate pertanto necessariamente dovrà variare la portata maltita dalla nuova girante nello stesso rapporto della variazione delle rispettive sezioni di passaggio dell’acqua e quindi anche nel rapporto dei rispettivi diametri. Detta la nuova portata potremo scrivere:
$\frac { { Q}_{11}}{{ Q}_{1}} =\frac { { 1}^{2}}{{ D}^{2}}$                 Q₁₁= $\frac { { Q}_{1}}{{ D}^{2}}$                       Q₁₁= $\bf\frac { { Q}_{1}}{{ D}^{2}\sqrt { H}}$
Siamo passati dal diametro D a quello di 1 m ed essendo le velocità le stesse per entrambe le giranti e quindi in particolare quella periferica, necessariamente dovrà modificarsi il numero di giri.
$\frac { {\large n}_{11}}{{\large n}_{1}} =\frac { D}{ 1}$                 n₁₁=n₁D                       n₁₁= $\bf\frac {{\large n}D}{\sqrt { H}}$
vengono definiti rispettivamente numero di giri specifico e portata specifica.
Essi rappresentano quindi il numero di giri e la portata che una girante dal diametro D=1 m e H=1 m deve operare per mantenere inalterate le condizioni di funzionamento iniziali di una girante simile con diametro D e salto H.

Esempio
Si abbia una turbina funzionante con i seguenti dati nominali:
H = 130 m Q= 25 m³/s   n= 500 rpm e diametro ruota D = 1,68 m
Dalle relazioni precedenti ricaviamo :
Q₁₁= 0,777    n₁₁= 73,673
La stessa ruota potrà essere utilizzata con nuovi valori di H, Q, n se Q₁₁ e n₁₁ rimarranno inalterati
Per esempio con H= 95 m   Q= 21,4 m³/s si ricaverà n=427 rpm

Numero di Giri Caratteristico
Una delle espressioni più usate per classificare una girante è quella che ci permette di calcolare il suo “ Numero di Giri Caratteristico” . Esso rappresenta la velocità n in rpm (revolution per minute) di una girante simile a quella che si considera sotto il salto di H = 1 m e la portata Q=1 m³/s. Tale numero si esprime con : n_q=n $\bf \frac {\sqrt{Q}}{ { H }_{ }^{ 0,75 } }$ [b]
Una prima classificazione può essere fatta conformemente alla tabella seguente :

nq = 6 ÷ 20	macchine motrici lente	Pelton
nq = 20 ÷ 100	macchine motrici medie	Francis
nq > 100	macchine motrici veloci	Kaplan

NB.
La classificazione lente, medie, veloci non è legato al numero di giri di funzionamento ma al valore di nq . A valori alti di nq corrispondono in genere numero di giri di funzionamento bassi ( Kaplan).

Con i dati dell’esempio precedente si ricava: n_q=500 $\frac {\sqrt {25}}{ { 130 }_{ }^{ 0,75 }}$ ≈ 65

Vediamo come si ricava l’espressione di n_q.
Sia data una turbina funzionante con H-Q-n e con ruota di diametro D. Alimentiamo la stessa ruota con H=1 m (ricaviamo Q₁ e n₁) e quindi con Q_c=1 m³/s . Utilizzando le relazioni precedenti possiamo scrivere:
$\frac { { Q}_{1}}{{ Q}_{c}} =\frac { { D}^{2}}{{ D}_{c}^{2}}$ $\frac { D}{{ D}_{c}}=\sqrt\frac { { Q}_{1}}{{ Q}_{c}}$ $\frac{ D}{{ D}_{c}}=\sqrt{\frac {{Q}_{1}}{1}}$ $\frac { D}{{ D}_{c}}=\sqrt{{\scriptsize Q}_{\scriptsize 1}}$
Parimenti
$\frac { {\large n}_{c}}{{\large n}_{1}} =\frac { D}{{ D}_{c}}$ ${ n}_{c}={n}_{\scriptsize 1}\sqrt {\scriptsize Q}_{\scriptsize 1}$ ${ n}_{c}=\frac { \large n}{\sqrt { H}}\sqrt{\frac { Q}{\sqrt { H}}}$

ponendo n_c=n_q ne deriva: n_q=n $\bf \frac { \sqrt{ Q}}{ { H }_{ }^{ 0,75 } }$
I costruttori di turbine idrauliche hanno a disposizione per una serie discreta di nq uno o più modelli testati in laboratorio. In funzione dei dati di progetto si calcola velocemente nq e si sceglierà quello più prossimo a disposizione. A questo punto il profilo idraulico della macchina industriale o in gergo prototipo si otterrà moltiplicando per il rapporto K=D_p/D_m i dati geometrici del modello (D_p= diametro ruota prototipo e D_m = diametro ruota modello).
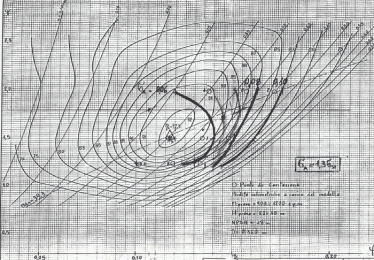
Le prove di laboratorio hanno soprattutto lo scopo di determinare i rendimenti che la turbina può fornire. Questa campagna di prove oltre a fornire numerose indicazioni di comportamento della turbina permette di disegnare un diagramma detto “ collinare “ vedi figura sotto, che in funzione di H e Q o altre grandezze a loro legate ci permettono di determinare il rendimento della turbina in quel punto di funzionamento. In genere il rendimento del prototipo è superiore rispetto a quello ottenuto dal modello perché per esempio le perdite di attrito nei passaggi idraulici hanno una influenza minore. Esistono varie formule di rivalutazione in funzione del tipo di turbina ma non è il caso di addentrarci in calcolazioni che vanno al di là dello scopo di questo sito.

Le prove su modello oltre ad essere un potente strumento di indagine per chi studia nuove macchine può essere altrettanto utile ed importante per i committenti che vogliono accertarsi prima della costruzione della turbina industriale il suo futuro comportamento su scala ridotta, ovvero testare la fascia di operazione a cui è chiamata ad operare la futura macchina. Una delle prove standard è quella di determinare in quali condizioni di salto e portata si maifesta la “Torcia” ovvero quella specie di coda di bollicine che si origina sotto la ruota. Tale fenomeno produce instabilità operativa e fluttuazioni di potenza più o meno evidenti. Nei filmati 1 e 2 si nota la ” Torcia” su due differenti test di modello di turbina Francis. Importante è accertarsi che l’ insorgere della torcia sia fuori dalla fascia normale di operazione. La torcia è tipica di macchine a reazione e non esiste ovviamente sulle Pelton.

Come sopra accennato i coefficienti che possono essere utilizzati per la determinazione degli assi di un collinare e/o di individuazione del tipo di macchina son vari. Nella tabella seguente si riportano quelli più utilizzati.

n_q=n $\bf \frac { \sqrt{ Q}}{ { H }_{ }^{ 0,75 } }$

n_s=n $\bf\frac { \sqrt{ P \bf\scriptsize (Kw) }}{ { H }_{ }^{ 1,25 } }$

n₁₁= $\bf\frac {{\large n}D}{\sqrt { H}}$

Q₁₁= $\bf\frac { Q}{{ D}^{2}\sqrt { H}}$

n_s= $\bf \scriptsize 3,1321\sqrt{\normalsize \eta}$ n_q

n_q= $\bf { n}_{\scriptsize 11}\sqrt {{\scriptsize Q}_{\scriptsize 11}}$

ns= $\bf\scriptsize 3,1321\sqrt{{\normalsize \eta}{ Q}_{11}}$ n₁₁

φ= $\bf\scriptsize 24,3171\frac{\normalsize Q}{{\normalsize D}^{\normalsize 3}\large n}$

ψ= $\bf\scriptsize 7153,60\frac{\normalsize H}{{\normalsize D}^{\normalsize 3}{\large n}^{\normalsize 2}}$

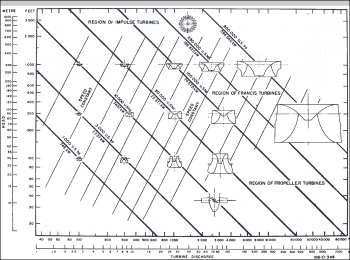
Le figure sottostanti danno un’ idea dei campi di applicazione delle varie tipologie di turbina

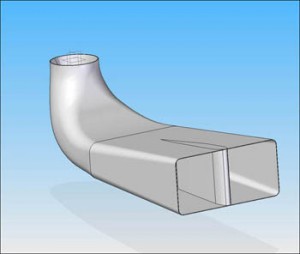
Gomito di Scarico
Quando abbiamo a che fare con le turbine a reazione un componente di grande importanza è costituito dal Gomito di Scarico a cui è demandato soprattutto il compito di recuperare l’energia cinetica all’uscita della girante in energia di pressione, ovvero recupero del salto che contrariamente andrebbe perso. Questa trasformazione diventa vitale nelle turbine a basso salto come per es. le Kaplan poiché la percentuale di energia persa sarebbe significativa comparata al salto disponibile. Detto D_s il diametro del gomito appena all’uscita della Girante la velocità con cui l’acqua lascia la ruota è v_s= $\bf\frac { 4Q }{{\large \pi }{ D }_{\large s }^{ 2 } }$ (m/s) e il corrispondente salto che andrebbe perso sarebbe H_p= $\bf\frac { {\large v }_{\large s }^{ 2 }}{\large 2g }$
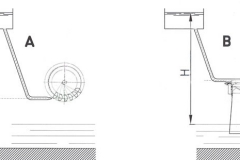
Una morfologia tipica è quella rappresentata dalle due immagini sotto

Fig. 7 (gomito.jpg)